Objective 7

 Problem Solving with Various Mathematical Tools

Theorems and Properties

Features:

• Fundamental laws such as commutative, associative, and distributive.
• Identity, dominance, absorption theorems, etc.

Gates:

• Representation of logical functions using AND, OR, NOT gates.
• Implementation in electronic circuits.

Principles of Duality:

• Relationship between dual operations like AND and OR, 1 and 0.
• Allows simplification of logical expressions by swapping operators and variables.

Combinatorial Circuits

Features:

• Design of circuits where the output depends solely on the current inputs.
• Examples include adders, decoders, multiplexers.

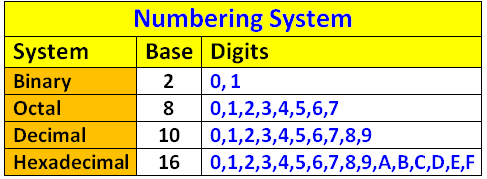
Numeric Systems

Binary, Octal, Hexadecimal:

• Representation of numbers in different numerical bases.
• Conversion between numerical bases and its significance in computing.

Numeric Representation:

• Meaning of bits and their representation in numerical systems.
• Importance of Most Significant Bit (MSB) and Least Significant Bit (LSB).

Base Conversion:

• Procedures for converting numbers between bases, such as the method of successive division.

Basic Operations and Matrix Theorems

Basic Operations:

• Addition, subtraction, multiplication, and division in different numerical bases.
• Application of algebraic laws in expression simplification.

Matrices and Matrix Algebra:

• Matrix operations such as addition, multiplication, inversion.
• Applications in systems of linear equations and linear transformations.

Recurrence Relations and Classical Problems

Recurrence Relations:

• Expressions that relate a term to previous terms in a sequence.
• Examples include the Fibonacci sequence and the Towers of Hanoi problem.

Fibonacci Sequence:

• Recursive definition and its relationship with the golden ratio.
• Applications in computer science, mathematics, and nature.

Towers of Hanoi:

• Description of the problem and its recursive solution.
• Examples of algorithmic implementations.

Ackermann Function

Ackermann Function:

• Mathematical definition of a recursively increasing function.
• Description of its properties and applications in theoretical computer science.